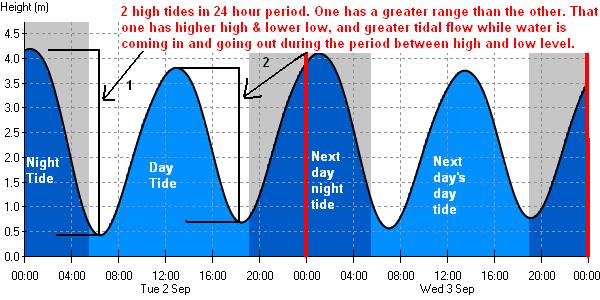
When you get into a tight place and everything goes against you, till it seems as though you could not hang on a minute longer, never give up then, for that is just the place and time that the tide will turn. -Harriet Beecher StoweLast week, our longtime reader Pamela asked if I could explain how the tides work. As you all know, when the tide comes in at the ocean, the water level appears to rise (and can do so significantly), while at low tide, the water level appears to drop.

This goes in a cycle twice per day, with the ocean level reaching its highest point twice daily (high tide), having the water recede over a period of six hours until it reaches its lowest level (low tide), and then having the water level rise again over a period of another six hours until it reaches the next high tide. Variations in the height of the water level are typically on the order of three meters (maybe ten feet) each day, depending on a couple of factors, which I'll go into below.
The reason we have any tides at all are twofold: the Earth is pretty big and gravity cares how far away you are. The farther away you are from something, the weaker gravity's pull is on you. If you were to take a look at our Solar System, and you were to move the Earth out to where Pluto is, you'd find that the force of gravity from the Sun on the Earth would be an astounding 1,600 times weaker than it is today, as Pluto is 40 times as far away as Earth is from the Sun!
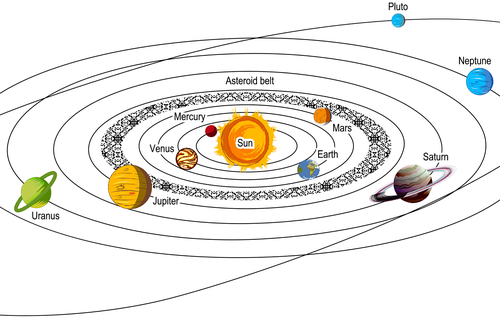
If you were to look at everything in our Solar System and ask what affects the Earth the most, gravitationally, you'd think to look at two things: the Moon, because it's massive and it's very, very close to us, and the Sun, because it's extremely massive, even though it's quite far away. Let's start by considering the Moon.

The Earth is quite far from the Moon, at an average distance of 384,400 km. When we speak about this distance, however, we are talking about the distance from the center of the Earth to the center of the Moon. But one edge of the Earth will always be closer to the Moon by 6,370 km (the radius of the Earth), and the opposite edge will always be farther from the Moon by the same amount. This means -- after a little math -- that the force of gravity of the Moon on the far side of the Earth is about 3.2% weaker at the far edge of the Earth than it is at the center of the Earth, and about 3.4% stronger at the edge of Earth nearest the Moon than it is at the center. This difference in forces between the near edge, the center, and the far edge defines what we call tidal forces.
This means the effect of the Moon's gravity on Earth is to try to flatten it a little bit at the poles and wherever Moonset/Moonrise is occurring, and to stretch it at its nearest point (when the Moon is directly overhead) and its farthest point (exactly 12 hours from the Moon's apex). This force is weak enough that it wouldn't be a big deal at all if the Earth were simply a solid ball; the tidal forces from the Moon are unable to stretch rocks and dirt by more than a few millimeters. But the Earth is covered in water, which changes its shape extremely easily!
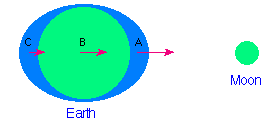
(Image Credit: Steve Gaunt.)
So while the solid ground of the Earth remains in its roughly spherical shape, the oceans bulge by just a few meters in two spots around the equator: at the point closest to the Moon and at the point farthest from the Moon. As the solid ground rotates, each point on the Earth passes through the side closest to the Moon and the side farthest from the Moon once per day: these are your two high tides.
The two times that correspond to Moonrise and Moonset are your two low tides per day. And the closer to the equator you are, the more severe your tides are, while the closer to the poles you are, the less drastic your tides are!
But the Moon isn't the only gravitational body in our Solar System affecting the tides on Earth. While none of the other planets, moons, asteroids or comets in the Solar System matter, the Sun does!

The tidal forces from the Sun are weaker than those from the Moon, but are still quite strong, causing tides that are about 30% as strong as the Moon's. When the Sun and the Moon are lined up, during a New Moon and during a Full Moon, you get the highest high tides and the lowest low tides, known as Spring Tides.
But when the Sun and Moon are at right angles to each other (during the Moon's first and last quarter, or when it appears half-full), you get the lowest high tides and the highest low tides, known as Neap Tides.
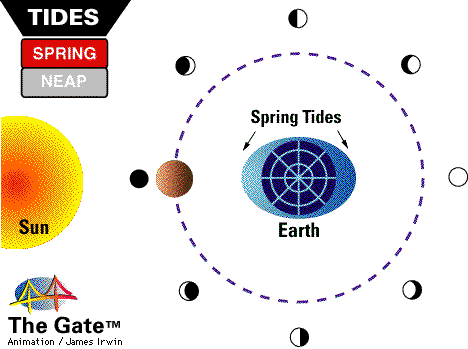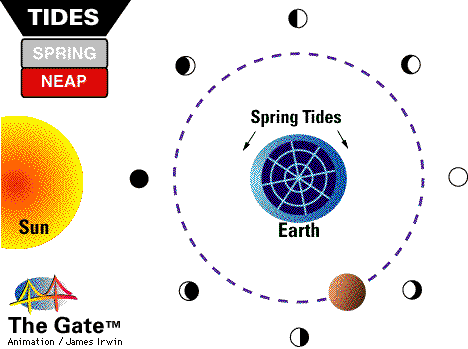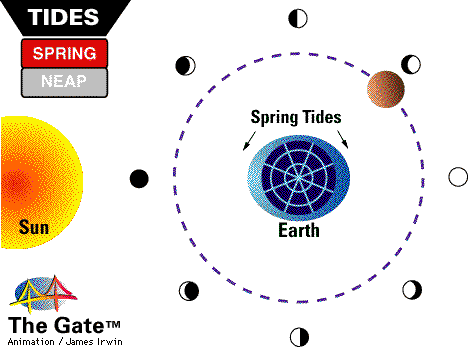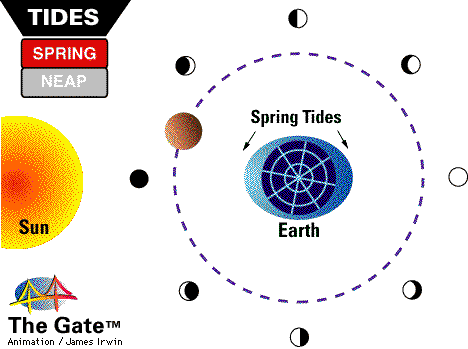
In fact, if you're meticulous, you can measure the water level over a long period of time, and can see not only the high tides and the low tides, but also where the Spring Tides and Neap Tides occur. Take a look at this data from Bridgeport, Connecticut.
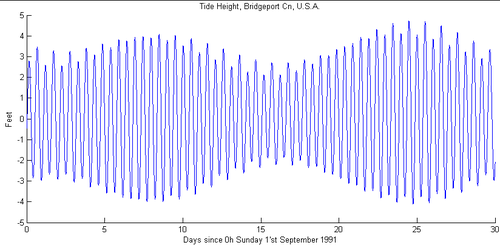
And that's how tides work! I freely admit that there are small, subtle details that come into play if you want to predict the times and heights of the tides extremely accurately. But just by considering the gravity of the Sun, Earth and Moon, and by calculating the force on the oceans, you can do an incredible job of predicting all of the above about the tides. Thanks to Pamela for a riveting question, and I hope you all enjoyed the answer!





Comments
THANK YOU, Ethan. The explanation and the graphics explain it so well!! Wonderful!
Posted by: Pammie | February 24, 2010 8:42 PM
Only one of your graphics is accurate; the other graphics (and your prose) explain two increasing tides, but don't explain the two decreasing tides!
In fact, many of your graphics are used as examples of common ways that textbooks botch coverage of tides. For more information, read Donald Simanek's page on the subject.
Posted by: John Armstrong | February 24, 2010 9:00 PM
The tides in St Vincent's Gulf in South Australia are interesting. At the suburban beaches of Adelaide, the tides occur at roughly the same time each day, regardless of the phase of the moon. The reason is that the resonant frequency of the Gulf is close to one day, so solar tides are amplified and are slightly higher amplitude than the lunar tides. But they are so close in amplitude that every fortnight they practically cancel each other out and the resulting almost complete absence of tide is called locally the dodge tides.
Posted by: Keith Harwood | February 24, 2010 9:12 PM
I am having trouble understanding why there would be a bulge on the opposite side to the moon (at point C in the 6th picture). Can anyone please explain that to me?
Posted by: Lindsay | February 24, 2010 9:41 PM
Your explanation makes it seem like the moon is literally pulling the water away from the Earth and hence the bulge. As I understand it, this is wrong (especially as the Sun has a stronger gravitational effect on the Earth than the Moon does). This might make sense to a layperson (myself being a layperson) but then why don't we get one bulge on the side closest to the moon?
I was under the impression that it had more to do with how the horizontal gravity vector actually pushes the water horizontally to where the furtherest and closest points to the moon are? Thus the water bulges due to being pushed sideways along the Earth to where the both high tides are.
I think another important point here is that the Sun exerts a much stronger gravitational force on the Earth than the Moon does. But, "... tidal force depends not on the strength of the lunar gravitational field, but on its gradient (which falls off approximately as the inverse cube of the distance to the originating gravitational body)"
http://en.wikipedia.org/wiki/Tide#Forces
The thing is that there is no simple explanation for tides! They are very complex mathematically and thus very hard to grasp - or that is at least what I think.
My head hurts :)
Posted by: Peter Si | February 24, 2010 10:01 PM
nice!
Posted by: Sophos | February 24, 2010 10:35 PM
@Linsey: let me give it a try...
Instead of the Earth and oceans, let's pretend we are dealing with three equal weights attached to a long rope (200km long), one in the middle of the rope and one on each end, stretched radially away from the moon.
The gravitational force experienced by the weights falls off as 1/R^2, so if the middle weight experiences a gravitational force A/R^2, the outer weight experiences a force of A/(R+100km)^2, which is less than the middle weight, and the inner weight experiences a force of A/(R-100km)^2, which is greater than the middle weight. Because all three must fall at the same rate (they are tied to each other, after all) the rope must be under tension.
If this rope contraption is in orbit around the moon such that the middle weight is in free-fall, and we adjust our point of view to be on the middle weight, then both the outer and inner weights will give the appearance of pulling away in opposite directions.
Looking at image 6, the three vectors are C = ->, B = -->, and A = --->. If you were to use a frame of reference which made the center of the Earth in free-fall, that would be the equivalent of adding -B = . Effectively, the water would be pulled radially outward by C', radially inward by A', and not at all by B'.
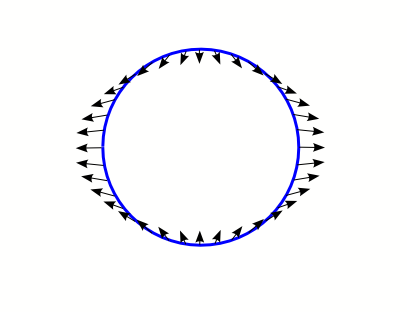
If, instead of a rope, you had a large ring, and you measured the pull of the moon's gravity (relative to the center of the ring) on various parts of the ring, you get a diagram like the 5th down. Every part of the ring experiences a tidal force which has a radial component away from the center of the ring, and tangentially towards the center of the ring. The tangential component comes from the fact that the moon's gravity is acting like it's coming from a point, so the forces on the ring are not parallel, but radiate from a point. This also contributes to the tidal flows.
Posted by: Blaise Pascal | February 24, 2010 10:47 PM
Blaise Pascal, thanks so much for that! I can make sense of it now.
Posted by: Lindsay | February 24, 2010 10:54 PM
I love your tides explanation. Nuances aside, it's a great illustration. But, I am confused by your statement that synchronizes low tides to moonrise and moonset. Checking the times for my location, these don't correspond at all. Are there further details that would explain that, or am I misunderstanding?
Posted by: Tavi Greiner | February 24, 2010 11:19 PM
@Tavi
There's always further details. For one thing the Earth doesn't spin freely under the oceans, but rather drags the oceans along with it. Water can't flow instantly either, so the end result is that instead of the tidal bulges being directly under the moon, they are slightly ahead of the moon by about 3 degrees, which means the tides arrive (in the deep ocean) about 12 minutes "fast".
For another, local coastal conditions have a major effect on the timing and size of tides. Keith Harwood described a situation where resonance affects the period of the tides, and the Bay of Fundy is famous for the shape of the bay greatly increasing the height of the tides.
Posted by: Blaise Pascal | February 24, 2010 11:44 PM
I used to get confused by the second bulge (opposite the Moon-side), but I've learned the key to remember is imaging the centripetal force "flinging" the water to the outside. Just like if you were to grab someone's hands and spin around (merrily), you would expect both participant's long hair would get swung to the "outside" (assuming they had long hair).
Remember, the Earth pulls on the Moon, and the Moon pulls back on the Earth, just like two people swinging around one another. And just like a very small person getting swung around by a very large person, they rotate around their common center of mass (barycenter). Like in these animations.
Posted by: Cody | February 24, 2010 11:45 PM
That's really good stuff. I had an argument with someone once, about what caused tides. While I did not have nearly the breadth of information that you did, my answer was basically "the moon and gravity". There response was that gravity isn't strong enough and the moon isn't big enough to cause that much of a chance, and when I asked them what they thought caused tides, they replied: "magnetism".
Posted by: dogmatichaos | February 24, 2010 11:54 PM
Blaise @10 and Tavi @9,
I read Tavi's comment this evening and was going to write a response, but before I got to it, Blaise's comment popped up.
Blaise, that is exactly what I would have hoped to have said. Your explanation, as far as I understand it, is dead on.
Posted by: Ethan Siegel | February 25, 2010 12:42 AM
John,
I don't understand your objection. Are you complaining that the other figures don't explain why there is a bulge along the Earth-Moon line, but no bulge perpendicular to it? If so, that's not an inaccuracy so much as an incompleteness, and I wouldn't call it a "botch" of anything.
Posted by: Ambitwistor | February 25, 2010 4:29 AM
Nice explanation. And I'm hesitant to complicate things too much, but I can't help myself:
I would point out that the image of the tides (ferinstance the one labelled "Steve Gaunt") are in disagreement with experimental observation. In fact, I’d venture that the OPPOSITE of that drawing is closer to the truth.
If you hang out for a day at the beach and watch the moon and the tides (on the day of a new moon, so you don’t have to worry about solar vs lunar tides) you will quickly find that high tide occurs pretty close in time to moonrise and moonset, and low tide occurs pretty close in time to the moon being overhead.
If you’re a landlubber, you can check out the tides online at, say, http://www.protides.com/hawaii/1332/ To simplify things, make sure to concentrate on a days with a new moon to avoid the complications of the solar and lunar tides fighting each other.
Your model is correct for a static earth and moon, but the actual dynamic system (where the ocean is resonantly-driven system) the response is almost (but not quite) 90-degrees out of phase with the drive. Which I think is some pretty neat physics as well.
Posted by: Anonymous Coward | February 25, 2010 3:10 PM
I'd add that local effects outweigh all the global effects considerably. Despite your statement that tides at the equator are bigger,here in the UK, tides are typically between 4 and 7 metres, whereas South Sea Islands seem to get about 1/2 a metre at most.
Posted by: davem | February 26, 2010 9:55 AM
@Davem
Actually, one of the sites I looked at had a FAQ of "Why aren't there tides at the equator?"
The answer was basically that the main axis of the ellipsoid of the oceans caused by the tides is aligned (roughly) with the moon, which is on an inclined orbit around the Earth. Because of various factors, this inclination is between 18 and 28degrees relative to the equator. Most of the time, the slice through this ellipsoid along the equatorial plane doesn't have a large amount of variation, so the tides at the equator are low.
I suppose that would suggest that when there is an eclipse on the equinox the equatorial tides are large.
Posted by: Blaise Pascal | February 26, 2010 2:53 PM